Одним из простых методов определения прогибов балки в определённой точки конструкции является графоаналитический метод. Данный метод в свое время был изложен в ряде книг по сопротивлению материалов, например в [1], [2].
      Графоаналитический метод основан на так называем дуализме физических соотношений, а именно на аналогии между дифференциальным уравнением, связывающим изгибающие моменты и нагрузку, и дифференциальным уравнением, связывающим прогибы и изгибающие моменты. 
      Как пишет С.П.Тимошенко [1] «… во многих случаях, в особенности, когда нам нужно знать скорее прогиб в определённой точке, чем общее [выражение] уравнение изогнутой оси балки, вычисление можно значительно упростить при помощи эпюры изгибающих моментов.»
      Рассмотрим этот метод подробнее.

Схема основных параметров  при изгибе бруса представлена на рис:

Рис.1. Схема деформирование бруса при изгибе

Здесь:

q(z) – поперечная нагрузка на балку в общем виде (функция от z)

f(z) – вертикальные перемещения упругой оси балки (прогибы, англ. flexion) (функция от z)

φ - угол наклона касательной к упругой оси балки в определённой точки (функция от z)

r - радиус кривизны (искривления) в определённой точки упругой линии балки (функция от z)

ϰ - кривизны (искривления) в определённой точки упругой линии балки (функция от z)

ϰ = 1/r [греч. «каппа»]

L – пролет балки

Рассмотрим дифференциальные уравнения, описывающие изгиб тонкого упругого бруса (балки):

f ' = φ                                                              (1)

φ' = М/EI                                                         (2)

М' = Q                                                             (3)

Q'= -q                                                             (4)

Подставляя (1) в (2) и (3) в (4), получаем:

f '' = М/EI                                                       (5)

М'' = -q                                                          (6)

Так же можно подставить (5) в (6) получая при этом известное дифференциальное уравнение изгиба упругой линии бруса

f ^IV= -q/EI                                                      (7)

здесь

Е – модуль упругости материала бруса

I – момент инерции сечения бруса

Решение уравнения (6), как мы знаем, находится известными методами интегрирования дифференциальных уравнения. Но также определить значение изгибающего момента М в каждой точке упругой линии бруса мы можем, используя уравнения статики, не прибегая к интегрированию.

Нетрудно заметить, что интегрирование уравнения (5) мы можем заменить статическим расчетом условной балки загруженной нагрузкой вида{-М}, полученные при этом значения моментов {m/EI} будут численно равны искомым значением перемещений f.

Таким образом интегрирование двух уравнения (5) и (6), либо одного уравнения (7) можно заменить двухэтапным статическим расчетом двух статически определимых балок: действительной и условной.

Иными словами:

Прогиб в произвольной точке упругой оси действительной балки (от заданной нагрузки) равен изгибающему моменту в той же точки условной балки (от условной нагрузки), деленному на жесткость действительной балки.

Угол поворота в произвольной точке упругой оси действительной балки (от заданной нагрузки) равен изгибающему моменту в той же точки условной балки (от условной нагрузки), деленному на жесткость действительной балки.

f = М_усл/EI                                                     (8)

φ= Q_усл/EI                                                      (9)

здесь М_усл и Q_усл значение изгибающих моментов и поперечных усилий полученные от загружения условной балки условной нагрузкой q_усл= (-М)

При переходе от расчета действительной балки к условной мы должны соблюсти опорные условия в условной балке, непосредственно вытекающие из (8) и (9):

1) если прогиб действительной балки f равен нулю, то в той же точке упругой линии условной балке условный изгибающий момент должен быть равен нулю;

2) если угол поворота действительной балки φ равен нулю, то в той же точке упругой линии условной балке условное поперечное усилие должно быть равен нулю;

         3) если прогиб или угол поворота действительной балки не равен нулю, то соответствующие им M_усл и Q_усл так же не должны быть равны нулю.  

табл. 1. Соответствие опорных условий действительной и условной балки. 

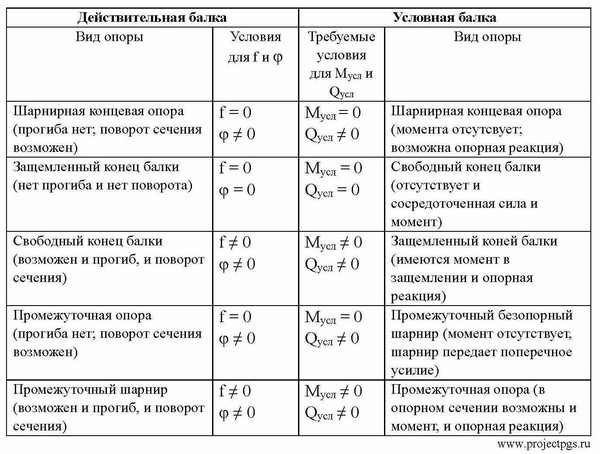
Таким образом, для того чтобы найти прогиб f или угол поворота φ какого-либо точки упругой линии заданной (действительной) балки, нужно последовательно выполнить следующие операции:

1) построить схему заданной балки с заданной нагрузкой;

2) построить эпюру изгибающего момента М(z);

3) принять нулевую линию эпюры М(z) за ось условной балки, а эпюру М(z), взятую с обратным знаком за условную нагрузку q_усл ;

4) задать опорные условия условной балки в соответствии с табл. 1;

5) определить опорные реакции в опорах условной балки от условной нагрузки (для балок, защемленных одним концом это допускается не производить);

6) Определить величину условного изгибающего момента M_усл в сечении условной балки с той же абсциссой, что и сечение, где отыскивается прогиб f;

7) Определить величину условного поперечного усилия Q_усл в сечении условной балки с той же абсциссой, что и сечение, где отыскивается угол поворота φ;

8) Определить f и φ по формулам (8) и (9)

Необходимо учесть, что все построения и расчеты необходимо производить в величинах одинаковой размерности.

       Касаясь истории появления графоаналитического метода С.П.Тимошенко пишет: «Применение эпюры изгибающих моментов к вычислению прогибов балок было разработано O. Mohr’ом, см. Z.Architect и Ing.-Ver. (Hannover), стр. 10, 1868, см. также его Abhandlung, стр. 294; цититированная на стр. 43. Подробный метод был разработан независимо профессором C.L.Green’ом. Univ. of Michigan, 1874. Кажется, что впервые этот метод был предложен St. Venart’ом. См. его замечания в книге Navier, стр. 72 и 79. Цитированные на стр. 103.»

Рассмотрим пример:

Определения прогибов в однопролетной шарнирно-опертой балки

Исходные данные:

Однопролетная балка, загруженная двумя симметрично расположенными силами P на расстоянии а от опоры.

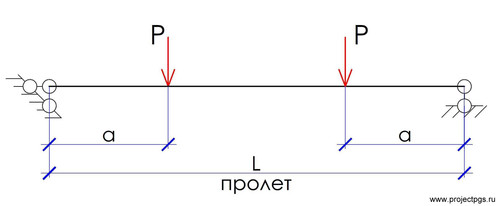
            Определим изгибающие моменты в указанной балке:

Используем М₀ = P · a в дальнейших рассуждениях как параметр.

Загрузим исходную балку нагрузкой по форме, совпадающей с эпюрой моментов в исходной балке.

          Для упрощения решения задачи, представим данное загружения как сумму двух компонент: равномерно распределённой нагрузки и загружения вблизи опор «треугольной» распределённой нагрузкой.

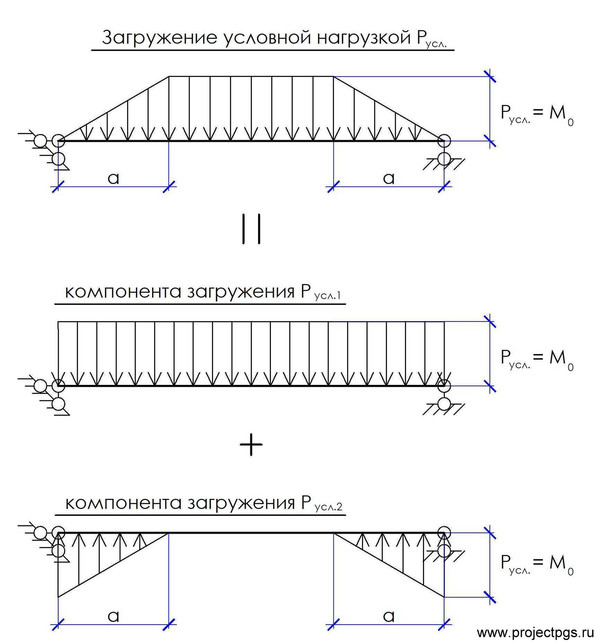
«Условный» изгибающий момент М_усл.1 для первой компоненты загружения возможно определить по раннее выведенной формулы моментов для равномерно-распределенной нагрузки.

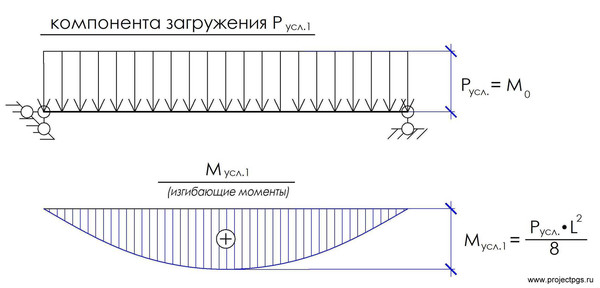
Определим «условный» момент М_усл.2 для второй компоненты загружения:

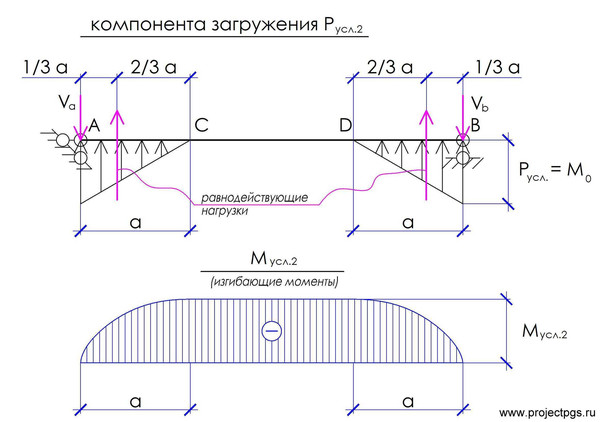
          Опорная реакция V_a = <равнодействующей> = ½· M₀· a

Тогда «условный» изгибающий момент в т. С (а также на участке C-D) равен

М _усл.2 = - V_a · a + V_a 2/3 · a  = - V_a · a · (1 – 2/3) = = - V_a · a / 3 =

= - ½· M₀ · a · a / 3 = - M₀ · a² / 6

Суммируя М _усл.1  и М _усл.2 получаем:

М _усл. =  М _усл.1  + М _усл.2 =  M₀ · L² / 8 - M₀· a² / 6 = M₀ · (L² / 8 - a² / 6 ) 

Подставляя M₀ = P· a

М _усл. = P · a · (L² / 8 - a² / 6)

Исходя из принципа w → М _усл  получаем:

w = P · a · (L² / 8 - a² / 6 ) / EI

Как нетрудно убедиться, данное соотношение точно совпадает с табличными соотношениями [3]

Литература

1. Беляев М.Н. Сопротивление материалов. М., Изд-во «Наука» 1965 г., 856 стр. с илл. 
2. Тимошенко С.П. Сопротивление материалов. Том 1. Элементарная теория и задачи. Изд-ва «Наука». Главная редакция физ.-математической литературы. Москва. 1965, 364 стр.
3. Справочник проектировщика промышленных, жилых и общественных зданий и сооружений. Расчетно-теоретический. Под ред. д.т.н проф. А.А.Уманского. М., Госстройиздат. 1960 г.